CBSE Class IX ( 9th) Science | Chapter 8. Motion | Lesson Exercises
Questions with in the Chapter
Answer : Yes, an object even after it has moved through a distance, it can have zero displacement. As we know distance is just length of the path an object has covered irrespective of its direction or position with reference to certain point, where as the shortest distance measured from the initial to the final position of an object is known as the displacement.
For example, an object starts from point A and after covering a distance of say 50 meters, reaches at point B. Here after, it again moves back to point A.
Here the distance covered by object is = AB + BA = 50 m + 50 m = 100 m
where as displacement of object is = AB - BA = 50 m - 50 m = 0 m
As initial position of object is same as that of its final position hence its displacement, which is distance measured from the initial to the final position, is zero.
Question 2. A farmer moves along the boundary of a square field of side 10 m in 40 s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position?
Answer : Suppose, a farmer moves along the boundary of a square field of side 10 m in 40 s as shown in the figure given below.
Which means the farmer will be at point C just diagonally opposite of point A
∴ Relative Displacement of farmer from point A at the end of 3 1/2 round will be = length of AC
which can be determined by the mathematical theorem as given below :
Question 3. Which of the following is true for displacement?
(a) It cannot be zero.
(b) Its magnitude is greater than the distance travelled by the object.
Answer : Both of the statements are not true as
(a) Displacement can be zero
(b) Its magnitude is either less or equal to the distance travelled by the object
------------------------------------------------------
Page 102 (CBSE Class IX ( 9th) Science Textbook - Chapter 8. Motion )
Question 1. Distinguish between speed and velocity.
Answer : The speed of an object is the distance covered per unit time,and velocity is the displacement per unit time. The speed is a scalar quantity as it has just magnitude where as velocity is a vector quantity as it has both direction as well as magnitude.The speed can be changed by the distance travelled by a body in a particular time where as the velocity can be changed by changing the object's speed, direction of motion or both.
Question 2. Under what condition(s) is the magnitude of average velocity of an object equal to its average speed?
Answer : The magnitude of average velocity of an object is equal to its average speed, only when it is moving in a straight line.
Question 3. What does the odometer of an automobile measure?
Answer : Odometer of an automobile measures the distance covered by an automobile. All Automobiles are fitted with Odometer. Earlier Odometer used to be mechanical device, now a days we have electronic odometer.
Question 4. What does the path of an object look like when it is in uniform motion?
Answer : The path of an object looks like a straight line when it is in uniform motion.j
Question 5. During an experiment, a signal from a spaceship reached the ground station in five minutes.
What was the distance of the spaceship from the ground station? The signal travels at the speed of light, that is, 3 × 108 m s-1
Answer :
--------------------------------------------------------------------
Page 103 (CBSE Class IX ( 9th) Science Textbook - Chapter 8. Motion )
Question 1. When will you say a body is in (i) uniform acceleration? (ii) nonuniform acceleration?
Answer : (i) A body is said to be in uniform acceleration if it travels in a straight line and
its velocity increases or decreases by equal amounts in equal intervals of time
(ii) A body is said to be in nonuniform acceleration if the rate of change of its velocity is not constant .
Question 2. A bus decreases its speed from 80 km h-1 to 60 km h-1 in 5 s.
Find the acceleration of the bus.
Answer :
Question 3. A train starting from a railway station and moving with uniform acceleration attains a speed 40 km h-1 in 10 minutes. Find its acceleration.
Answer :
--------------------------------------------------------------------
Page 107 (CBSE Class IX ( 9th) Science Textbook - Chapter 8. Motion )
Question 1. What is the nature of the distance-time graphs for uniform and non-uniform motion of an object?
Answer :
(i) For uniform speed, a graph of distance travelled against time is a straight line and not inclined along the time axis, as shown in the figure below (iI) For uniform speed, a graph of distance travelled against time is a curve and as shown in the figure below
Question 2. What can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis? Answer : Motion of an object whose distance-time graph is a straight line parallel to the time axis is not moving at all and is in state of rest as shown in the figure below : Question 3. What can you say about the motion of an object if its speed-time graph is a straight line parallel to the time axis?
Answer :The motion of an object if its speed-time graph is a straight line parallel to the time axis indicates that the object is moving with uniform speed.
Question 4. What is the quantity which is measured by the area occupied below the velocity-time graph?
Answer :The area occupied below the velocity-time graph measures the distance covered by the object.
--------------------------------------------------------------------
Question 1. A bus starting from rest moves with a uniform acceleration of 0.1 m s-2 for 2 minutes.
Find (a) the speed acquired, (b) the distance travelled.
Answer :
Question 2. A train is travelling at a speed of 90 km h1 Brakes are applied so as to produce a uniform acceleration of -0.5 m s-2 Find how far the train will go before it is brought to rest.
Answer :
Question 3. A trolley, while going down an inclined plane, has an acceleration of 2 cm s-2. What will be its velocity 3 s after the start?
Answer :
Question 4. A racing car has a uniform acceleration of 4 m s-2. What distance will it cover in 10 s after start?
Answer :
Question 5. A stone is thrown in a vertically upward direction with a velocity of 5 m s-1If the acceleration of the stone during its motion is 10 m s-2 in the downward direction, what will be the height attained by the stone and how much time will it take to reach there?
Answer:
------------------------------------------
Exercises (CBSE Class IX ( 9th) Science Chapter 8. Motion)
Question 1. An athlete completes one round of a circular track of diameter 200 m in 40 s. What will be the distance covered and the displacement at the end of 2 minutes 20 s? Distance covered by the athlete
Answer :
Question 2. Joseph jogs from one end A to the other end B of a straight 300 m road in 2 minutes 30 seconds and then turns around and jogs 100 m back to point C in another 1 minute.
What are Joseph.s average speeds and velocities in jogging (a) from A to B and (b) from A to C?
Answer :
Question 3. Abdul, while driving to school, computes the average speed for his trip to be 20 km h-1 On his return trip along the same route, there is less traffic and the average speed is 30 km h-1 What is the average speed for Abdul.s trip?
Answer : Let us assume:
Question 4. A motorboat starting from rest on a lake accelerates in a straight line at a constant rate of 3.0 m s-2 for 8.0 s. How far does the boat travel during this time?
Answer :
Question 5. A driver of a car travelling at 52 km h-1 applies the brakes and accelerates uniformly in the opposite direction. The car stops in 5 s. Another driver going at 3 km h-1 in another car applies his brakes slowly and stops in 10 s. On the same graph paper, plot the speed versus time graphs for the two cars. Which of the two cars travelled farther after the brakes were applied?
Answer : As given in the figure below AB (in red line) and CD(in red line) are the Speed-time graph for given two cars with initial speeds 52 kmh-1 and 3 kmh-1 respectively.
Question 6. Fig 8.11 shows the distance-time graph of three objects A,B and C. Study the graph and answer the following questions:
(a) Which of the three is travelling the fastest?
(b) Are all three ever at the same point on the road?
(c) How far has C travelled when B passes A?
(d) How far has B travelled by the time it passes C?
Answer :Drawing x and y coordinates from points A, B and C we get :
(a) Object B is travelling the fastest
(b) None of three are ever at the same point on the road as their graph LM, OB and LC do not coincided simultaneously at any point.
(c) C has travelled a distance JK = IM-KM = 9.14-1.14 km =8 km when B passes A.
(d) B has travelled a distance XY = 6 km when B passes C.
Question 7. A ball is gently dropped from a height of 20 m. If its velocity increases uniformly at the rate of 10 m s-2, with what velocity will it strike the ground? After what time will it strike the ground?
Answer :
Let us assume, the final velocity with which ball will strike the ground be 'v' and time it takes to strike the ground be 't'
Question 8. The speed-time graph for a car is shown is Fig. 8.12.
(a) Find how far does the car travel in the first 4 seconds. Shade the area on the graph that represents the distance travelled by the car during the period.
(b) Which part of the graph represents uniform motion of the car?
Answer :
(a)The shaded area with blue color under Speed-time graph represents the distance which the car will travel in first 4 second.
(b) The straight line part of graph, from point A to point B represents a uniform motion.
Question 9. State which of the following situations are possible and give an example for each of these:
(a) an object with a constant acceleration but with zero velocity
(b) an object moving in a certain direction with an acceleration in the perpendicular direction.
Answer : Both the situations are possible.
(a) An object with a constant acceleration can still have the zero velocity. For example an object which is at rest on the surface of earth will have zero velocity but still being acted upon by the gravitational force of earth with an acceleration of 9.81 ms-2 towards the center of earth.
(b) When an athlete moves with a velocity of constant magnitude along the circular path, the only change in his velocity is due to the change in the direction of motion. Here, the motion of the athlete moving along a circular path is, therefore, an example of an accelerated motion where acceleration is always perpendicular to direction of motion of an object at a given instance. .
Question 10. An artificial satellite is moving in a circular orbit of radius 42250 km. Calculate its speed if it takes 24 hours to revolve around the earth.
Answer : Let us assume An artificial satellite, which is moving in a circular orbit of radius 42250 km covers a distance 's' as it revolve around earth with speed 'v' in given time 't' of 24 hours.
= 42250 km
Page 100 (CBSE Class IX ( 9th) Science Textbook - Chapter 8. Motion )
Question 1. An object has moved through a distance. Can it have zero displacement? If yes, support your answer with an example.Answer : Yes, an object even after it has moved through a distance, it can have zero displacement. As we know distance is just length of the path an object has covered irrespective of its direction or position with reference to certain point, where as the shortest distance measured from the initial to the final position of an object is known as the displacement.
For example, an object starts from point A and after covering a distance of say 50 meters, reaches at point B. Here after, it again moves back to point A.
Here the distance covered by object is = AB + BA = 50 m + 50 m = 100 m
where as displacement of object is = AB - BA = 50 m - 50 m = 0 m
As initial position of object is same as that of its final position hence its displacement, which is distance measured from the initial to the final position, is zero.
| A | >-----------50 m-------------> <-----------50 m-------------< | B |
Question 2. A farmer moves along the boundary of a square field of side 10 m in 40 s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position?
Answer : Suppose, a farmer moves along the boundary of a square field of side 10 m in 40 s as shown in the figure given below.
Distance cover by the farmer as he moves from A to B to C to D to A, along the boundary wall of square field | = Perimeter of Square field | |
| = 4 x side of square field | ||
| = 4 × 10 m | ||
| = 40 m | ||
| ∴ speed of farmer | = 40 m/40 s | |
| = 1 m/s | ||
Distance covered by farmer in 2 minutes 20 seconds | = Speed × Time | |
| = 1 m/s × [(2×60) s + 20 s] | ||
| = 140 m | ||
Number of round in covering 40 m of distance along the boundary wall | = 1 round | |
∴ Number of round in covering 140 m of distance along the boundary wall | = 1×140 /40 rounds | |
| = 3.5 round | ||
| = 3 1/2 rounds |
which can be determined by the mathematical theorem as given below :
| AC | = √AB2 + √BC2 |
| = √102 + √102 | |
| =10 √22 | |
| = 10 × 1.414 m | |
| = 14.14m |
Question 3. Which of the following is true for displacement?
(a) It cannot be zero.
(b) Its magnitude is greater than the distance travelled by the object.
Answer : Both of the statements are not true as
(a) Displacement can be zero
(b) Its magnitude is either less or equal to the distance travelled by the object
------------------------------------------------------
Page 102 (CBSE Class IX ( 9th) Science Textbook - Chapter 8. Motion )
Question 1. Distinguish between speed and velocity.
Answer : The speed of an object is the distance covered per unit time,and velocity is the displacement per unit time. The speed is a scalar quantity as it has just magnitude where as velocity is a vector quantity as it has both direction as well as magnitude.The speed can be changed by the distance travelled by a body in a particular time where as the velocity can be changed by changing the object's speed, direction of motion or both.
Question 2. Under what condition(s) is the magnitude of average velocity of an object equal to its average speed?
Answer : The magnitude of average velocity of an object is equal to its average speed, only when it is moving in a straight line.
Question 3. What does the odometer of an automobile measure?
Answer : Odometer of an automobile measures the distance covered by an automobile. All Automobiles are fitted with Odometer. Earlier Odometer used to be mechanical device, now a days we have electronic odometer.
Question 4. What does the path of an object look like when it is in uniform motion?
Answer : The path of an object looks like a straight line when it is in uniform motion.j
Question 5. During an experiment, a signal from a spaceship reached the ground station in five minutes.
What was the distance of the spaceship from the ground station? The signal travels at the speed of light, that is, 3 × 108 m s-1
Answer :
| Speed of Signal (v) | = Speed of light |
| =3 × 108 ms-1 | |
| Time taken by Signal to reach the ground station (t) | = 5 minutes |
| = 5 × 60 seconds | |
| = 300 seconds | |
| Distance between the spaceship and the ground station (S) | = vt |
| = 3 × 108 m s-1 × 300 m | |
| =9×1010 m |
Page 103 (CBSE Class IX ( 9th) Science Textbook - Chapter 8. Motion )
Question 1. When will you say a body is in (i) uniform acceleration? (ii) nonuniform acceleration?
Answer : (i) A body is said to be in uniform acceleration if it travels in a straight line and
its velocity increases or decreases by equal amounts in equal intervals of time
(ii) A body is said to be in nonuniform acceleration if the rate of change of its velocity is not constant .
Question 2. A bus decreases its speed from 80 km h-1 to 60 km h-1 in 5 s.
Find the acceleration of the bus.
Answer :
| Initial Speed of the Bus (u) | = 80 km h-1 |
| = (80 × 1000)/ (60 × 60) ms -1 | |
| = 800/36 ms -1 | |
| Final Speed of the Bus (v) | = 60 km h-1 |
| = (60 × 1000)/ (60 × 60) ms -1 | |
| = 600/36 ms -1 | |
| Time in transition (t) | = 5 s |
| The acceleration of the Bus (a) | = (v-u) / t = [(800/36) - (600/36)] / 5 ms -2 = (-200/36) / 5 ms -2 = 5.55 / 5 ms -2 = 1.11 ms -2 |
Answer :
| Initial Speed of the Train (u) | = 0 ms -1 |
| Final Speed of the Train (v) | = 40 km h-1 |
| = (40 × 1000)/ (60 × 60) ms -1 | |
| = 400/36 ms -1 | |
| Time in transition (t) | = 10 minutes |
| = 10 × 60 s | |
| = 600 s | |
| = 600 s | |
| = 600 s | |
| The acceleration of the Train (a) | = (v-u) / t = [(400/36) - 0] / 600 ms -2 = (11.11) / 600 ms -2 = 0.0185 ms -2 |
Page 107 (CBSE Class IX ( 9th) Science Textbook - Chapter 8. Motion )
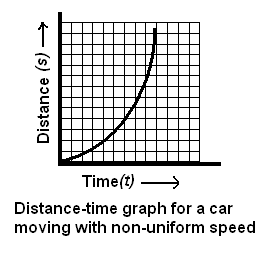
Question 1. What is the nature of the distance-time graphs for uniform and non-uniform motion of an object?
Answer :
(i) For uniform speed, a graph of distance travelled against time is a straight line and not inclined along the time axis, as shown in the figure below (iI) For uniform speed, a graph of distance travelled against time is a curve and as shown in the figure below
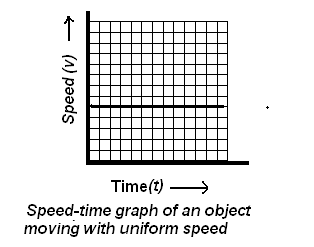
Question 2. What can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis? Answer : Motion of an object whose distance-time graph is a straight line parallel to the time axis is not moving at all and is in state of rest as shown in the figure below : Question 3. What can you say about the motion of an object if its speed-time graph is a straight line parallel to the time axis?
Answer :The motion of an object if its speed-time graph is a straight line parallel to the time axis indicates that the object is moving with uniform speed.
Question 4. What is the quantity which is measured by the area occupied below the velocity-time graph?
Answer :The area occupied below the velocity-time graph measures the distance covered by the object.
--------------------------------------------------------------------
Page 109-110 (CBSE Class IX ( 9th) Science Textbook - Chapter 8. Motion )
Question 1. A bus starting from rest moves with a uniform acceleration of 0.1 m s-2 for 2 minutes.
Find (a) the speed acquired, (b) the distance travelled.
Answer :
| Here as given, Initial speed (u) | = 0 | |
| Acceleration (a) | =0.1 m s-2 | |
| Time in transition (t) | =2 minutes | |
| =2 × 60 seconds= 120 s | ||
| We know that Final speed | = u + at | |
| ∴ (a) the speed acquired | = 0 + 0.1 m s-2 × 120 m s-1 | |
| = (1/10)120 ms-1 | ||
| = 12 ms-1 | ||
| = ut + (1/2)at2 | |
| ∴ (b) the distance travelled. | = 0 ×120 + (1/2) × 0.1×(120)2 | |
| = 0 + (120 × 120) /2 × 10 | ||
| = 14400/20 = 720 m | ||
| =720 m |
Question 2. A train is travelling at a speed of 90 km h1 Brakes are applied so as to produce a uniform acceleration of -0.5 m s-2 Find how far the train will go before it is brought to rest.
Answer :
| Given Initial speed of train (u) | =90 km h-1 |
| = (90 1000) / (60×60) m s-1 | |
| = 25 m s-1 | |
| Final speed of train (v) | = 0 ms1 |
| Braking acceleration (a) | = -0.5 m s-2 |
| We know 2as | = v2- u2 |
| Or distance (s) | =(v2-u2)/2a |
| ∴ Distance covered by the train before it came to rest | =(02-252)/(2 ×-0.5 )m |
| = - (25 × 25)×10/-1 m | |
| =625 m | |
Answer :
| Initial Velocity of trolley (u) | =0 cms-1 |
| Acceleration (a) | = 2 cm s-2 |
| Time (t) | = 3 s |
| We know that final velocity (v) | = u + at |
| = 0 + 2 x 3 cms-1 | |
| ∴ The velocity of train after 3 seconds | = 6 cms-1 |
Question 4. A racing car has a uniform acceleration of 4 m s-2. What distance will it cover in 10 s after start?
Answer :
| Initial Velocity of the car (u) | =0 ms-1 |
| Acceleration (a) | = 4 m s-2 |
| Time (t) | = 10 s |
| We know Distance (s) | = ut + (1/2)at2 |
| ∴ Distance covered by car in 10 second | = 0 × 10 + (1/2) × 4 × 102 |
| = 0 + (1/2) × 4× 10 × 10 m | |
| = (1/2)× 400 m | |
| = 200 m |
Answer:
| Given Initial velocity of stone (u) | =5 m s-1 |
| Downward of negative Acceleration (a) | = 10 m s-2 |
| We know that 2 (a)(s) | = v2- u2 |
| ∴Height attained by the stone (s) | = (02-52)/ 2 × (-10)m |
| = -25/-20 m | |
| = 1.25 m | |
| Also we know that final velocity (v) | = u + at |
| or Time (t) | = (v-u)/a |
| ∴ Time (t) taken by stone to attain the height(s) | = (0-5)/- 10 s |
| = 0.5 s |
Exercises (CBSE Class IX ( 9th) Science Chapter 8. Motion)
Question 1. An athlete completes one round of a circular track of diameter 200 m in 40 s. What will be the distance covered and the displacement at the end of 2 minutes 20 s? Distance covered by the athlete
Answer :
| Diameter of circular track (D) | = 200 m |
| Radius of circular track (r) | = 200/2=100 m |
| Time taken by the athlete for one round (t) | = 40 s |
| Distance covered by athlete in one round (s) | = 2π r |
| = 2 × ( 22 / 7 )×100 | |
| Speed of the athlete (v) | = Distance / Time |
| = (2 × 2200)/(7 × 40) | |
| = 4400 / 7 × 40 | |
| ∴ Distance covered in 2 minutes 20 seconds (s) or 140 s | = Speed (s) × Time(t) |
| = 4400 / (7 × 40) × (2×60 + 20) | |
| = 4400 /( 7 × 40) × 140 | |
| = 4400 × 140 /7 × 40 | |
| =2200 m | |
| Number of round in 40 s | =1 round |
| Number of round in 140 s | =140/40 |
| =3 1/2 | |
| After taking start from position X, the athlete will be at postion Y after 3 1/2 rounds as shown in figure | |
| ∴ Hence Displacement of the athlete with respect to initial position at X | =XY |
| = Diameter of circular track | |
| = 200 m |
Question 2. Joseph jogs from one end A to the other end B of a straight 300 m road in 2 minutes 30 seconds and then turns around and jogs 100 m back to point C in another 1 minute.
What are Joseph.s average speeds and velocities in jogging (a) from A to B and (b) from A to C?
Answer :
| Total Distance covered from AB | = 300 m |
| Total time taken | = 2 × 60 + 30 s |
| =150 s | |
|
| |
| ∴ Average Speed from AB | = Total Distance / Total Time |
| =300/150 m s-1 | |
| =2 m s-1 | |
| ∴ Velocity from AB | =Displacement AB / Time = 300/150 m s-1 |
| =2 m s-1 | |
| Total Distance covered from AC | =AB + BC |
| =300 + 200 m | |
| Total time taken from A to C | = Time taken for AB + Time taken for BC |
| = (2×60+30)+60 s | |
| = 210 s | |
| ∴Average Speed from AC | = Total Distance /Total Time |
| = 400 /210 m s-1 | |
| = 1.904 m s-1 | |
| Displacement (S) from A to C | = AB - BC |
| = 300-100 m | |
| = 200 m | |
| Time (t) taken for displacement from AC | = 210 s |
| ∴Velocity from AC | = Displacement (s) / Time(t) |
| = 200 / 210 m s-1 | |
| = 0.952 m s-1 |
Question 3. Abdul, while driving to school, computes the average speed for his trip to be 20 km h-1 On his return trip along the same route, there is less traffic and the average speed is 30 km h-1 What is the average speed for Abdul.s trip?
Answer : Let us assume:
The distance Abdul commutes while driving from Home to School | = S |
| Let us assume time taken by Abdul to commutes this distance | = t1 |
| Distance Abdul commutes while driving from School to Home | = S |
| Let us assume time taken by Abdul to commutes this distance | = t2 |
| Average speed from home to school v1av | = 20 km h-1 |
| Average speed from school to home v2av | = 30 km h-1 |
| Also we know Time taken form Home to School t1 | =S/v1av |
| Similarly Time taken form School to Home t2 | =S/v2av |
| Total distance from home to school and backward | = 2 S |
| Total time taken from home to school and backward (T) | = S/20+ S/30 |
| ∴ Average speed (Vav) for covering total distance (2S) | = Total Dostance/Total Time |
| = 2S/(S/20 +S/30) | |
| = 2S/[(30S+20S)/600] | |
| = 1200S/50S | |
| = 24 kmh-1 |
Special note regarding answer to above question :
The answer expressed above is a Harmonic Mean of average speeds of 20 kmh-1 and 30 kmh-1 not the Arithmetic Mean i.e. [(20+30) / 2]= 25 kmh-1.
How exactly does one find the average of two speeds travelled over equal distance. As given in above sum, Abdul first drive at an average speed of 20 kmh-1 and then travel back to home at an average speed of 30 kmh-1, to find out average speed for the whole trip, our first temptation will be to find out the Arithmetic Mean of two average speeds i.e. just to add 20 kmh-1 and 30 kmh-1 and then divide by 2 , giving the result 25 kmh-1 Which is quite obvious, but incorrect.
|
Question 4. A motorboat starting from rest on a lake accelerates in a straight line at a constant rate of 3.0 m s-2 for 8.0 s. How far does the boat travel during this time?
Answer :
| Given Initial velocity of motorboat u | = 0 |
| Acceleration of motorboat a | = 3.0 m s-2 |
| Time under consideration t | = 8.0 s |
| We know that Distance s | = ut + (1/2)at2 |
| ∴ The distance travel by motorboat | = 0 × 8 + (1/2)3.0 × 8 2 |
| = (1/2) × 3 × 8 × 8 m | |
| = 96 m |
Question 5. A driver of a car travelling at 52 km h-1 applies the brakes and accelerates uniformly in the opposite direction. The car stops in 5 s. Another driver going at 3 km h-1 in another car applies his brakes slowly and stops in 10 s. On the same graph paper, plot the speed versus time graphs for the two cars. Which of the two cars travelled farther after the brakes were applied?
Answer : As given in the figure below AB (in red line) and CD(in red line) are the Speed-time graph for given two cars with initial speeds 52 kmh-1 and 3 kmh-1 respectively.
| Distance Travelled by first car before coming to rest | =Area of △ OAB |
| = (1/2) × OB× OA | |
| = (1/2) × 5 s × 52 kmh-1 | |
| = (1/2) × 5× (52×1000)/3600) m | |
| = (1/2) × 5× (130/9) m | |
| = 325/9 m | |
| = 36.11 m | |
| Distance Travelled by second car before coming to rest | =Area of △ OCD |
| = (1/2) × OD× OA | |
| = (1/2) × 10 s× 3 kmh-1 | |
| = (1/2) × 10× (3×1000)/3600) m | |
| = (1/2) × 10× (5/6) m | |
| = 5× (5/6) m | |
| = 25/6 m | |
| = 4.16 m |
∴Clearly the first car will travel farther (36.11 m) than the first car (4.16 m).
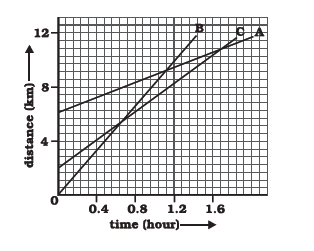
Question 6. Fig 8.11 shows the distance-time graph of three objects A,B and C. Study the graph and answer the following questions:
(a) Which of the three is travelling the fastest?
(b) Are all three ever at the same point on the road?
(c) How far has C travelled when B passes A?
(d) How far has B travelled by the time it passes C?
Answer :Drawing x and y coordinates from points A, B and C we get :
| Speed of object A | = Slope of MA |
| = AP / MP | |
| = 4/2.2 kmh-1 | |
| = 1.81 kmh-1 | |
| Speed of object B | = Slope of OB |
| = BQ / OQ | |
| = 12/1.4 kmh-1 | |
| = 8.57 kmh-1 | |
| Speed of object C | = Slope of LC |
| = CR / LR | |
| = 8/1.4 kmh-1 | |
| = 5.71 kmh-1 |
(b) None of three are ever at the same point on the road as their graph LM, OB and LC do not coincided simultaneously at any point.
(c) C has travelled a distance JK = IM-KM = 9.14-1.14 km =8 km when B passes A.
(d) B has travelled a distance XY = 6 km when B passes C.
Question 7. A ball is gently dropped from a height of 20 m. If its velocity increases uniformly at the rate of 10 m s-2, with what velocity will it strike the ground? After what time will it strike the ground?
Answer :
Let us assume, the final velocity with which ball will strike the ground be 'v' and time it takes to strike the ground be 't'
| Initial Velocity of ball u | =0 |
| Distance or height of fall s | =20 m |
| Downward acceleration a | =10 m s-2 |
| As we know, 2as | =v2-u2 |
| v2 | = 2as+ u2 |
| = 2×10×20 + 0 | |
| = 400 | |
| ∴ Final velocity of ball, v | = 20 ms-1 |
| t | = (v-u)/a |
| ∴Time taken by the ball to strike | = (20-0)/10 |
| = 20/10 | |
| = 2 seconds |
Question 8. The speed-time graph for a car is shown is Fig. 8.12.
(a) Find how far does the car travel in the first 4 seconds. Shade the area on the graph that represents the distance travelled by the car during the period.
(b) Which part of the graph represents uniform motion of the car?
Answer :
(a)The shaded area with blue color under Speed-time graph represents the distance which the car will travel in first 4 second.
(b) The straight line part of graph, from point A to point B represents a uniform motion.
Question 9. State which of the following situations are possible and give an example for each of these:
(a) an object with a constant acceleration but with zero velocity
(b) an object moving in a certain direction with an acceleration in the perpendicular direction.
Answer : Both the situations are possible.
(a) An object with a constant acceleration can still have the zero velocity. For example an object which is at rest on the surface of earth will have zero velocity but still being acted upon by the gravitational force of earth with an acceleration of 9.81 ms-2 towards the center of earth.
(b) When an athlete moves with a velocity of constant magnitude along the circular path, the only change in his velocity is due to the change in the direction of motion. Here, the motion of the athlete moving along a circular path is, therefore, an example of an accelerated motion where acceleration is always perpendicular to direction of motion of an object at a given instance. .
Question 10. An artificial satellite is moving in a circular orbit of radius 42250 km. Calculate its speed if it takes 24 hours to revolve around the earth.
Answer : Let us assume An artificial satellite, which is moving in a circular orbit of radius 42250 km covers a distance 's' as it revolve around earth with speed 'v' in given time 't' of 24 hours.
= 42250 km
| Radius of circular orbit r | |
| = 42250 × 1000 m | |
| Time taken by artificial satellite t | = 24 hours |
| = 24 × 60 × 60 s | |
| Distance covered by satellite s | =circumference of circular orbit |
| =2π r | |
| ∴ Speed of sattellite v | =(2π r)/t |
| =[2× (22/7)×42250 × 1000] / (24 × 60 × 60) | |
| =(2×22×42250×1000) / (7 ×24 × 60 × 60) m s -1 | |
| =3073.74 m s -1 |